##QUESTION
定义一个函数，输入一个链表的头结点，反转该链表并输出反转后链表的头结点。

##SOLUTION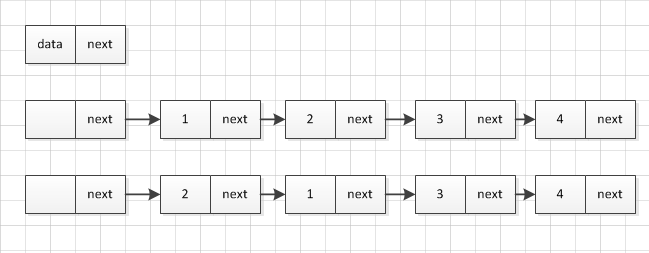

反转这个单链表的基本思想是，不断地将后面的结点移到head后面来，下面以反转结点1和结点2作为例子：

• 头结点的next指向结点2
• 结点1的next指向结点3
• 结点2的next指向结点1

这样就完成了一次交换，顺序变成了head->结点2->结点1->结点3->结点4->NULL，下面我们进行相同的操作将结点3移到head之后，然后将结点4移到head之后，就完成了反转，下面是代码：

typedef struct Node
{
    int data;
    struct Node *next;
}*node;

node reverse_list(node head)
{
    node p, q;
    if(head == NULL)
        return NULL;
    printf("the old list is:");
    print_list(head);

    p = head->next;
    while(p != NULL && p->next != NULL)
    {
        q = p->next;
        p->next = q->next;
        q->next = head->next;
        head->next = q;
    }
    return head； //可有可无   
}

题目的要求是返回新链表的头结点，在这里，新链表的头结点就是原来链表的头结点。所以最后一句是没有必要的，直接用head作为参数就可以打印链表。

##QUESTION
给定单项链表的头指针和一个结点指针，定义一个函数在O(1)时间删除该节点。

##O(n)解法
O(n)解法就是常规的删除链表结点的做法。从链表的头结点开始，顺序遍历查找要删除的结点，并在链表中删除该结点。这种思路由于要顺序查找，时间复杂度自然就是O(n)了。

之所以要从头开始查找，是因为我们需要得到将被删除的结点的前面一个结点。在单向链表中，结点中没有指向前一个结点的指针，所以只好从链表的头结点开始顺序查找。

##O(1)解法
那是不是一定要得到被删除结点的前一个节点呢？答案是否定的。我们可以这样来删除一个结点，例子如下，别删除的结点为i，i的下一个结点为j：

• 把j结点的内容复制到i结点，覆盖i结点的内容
• 将i结点的next指向j结点的next
• 删除j结点

这里我们删除的虽然是j结点，但是得到的效果却是删除了i结点。

还有一个问题，当我们删除的结点是尾结点时，尾结点的next是NULL，上述解法就不再适用，我们还是要顺序遍历后删除尾结点。

代码如下：

typedef struct Node
{
    int data;
    struct Node *next;
}*node;

/*在O(1)时间删除结点*/
void DeleteNode(node &pListHead, node pToBeDeleted)
{
    if(!pListHead || !pToBeDeleted)
        return;

    // 要删除的结点不是尾结点
    if(pToBeDeleted->next!= NULL)
    {
        node pNext = pToBeDeleted->next;
        pToBeDeleted->data= pNext->data;
        pToBeDeleted->next = pNext->next;

        delete pNext;
        pNext = NULL;
    }
    // 链表只有一个结点，删除头结点（也是尾结点）
    else if(pListHead == pToBeDeleted)
    {
        delete pToBeDeleted;
        pToBeDeleted = NULL;
        pListHead = NULL;
    }
    // 链表中有多个结点，删除尾结点
    else
    {
        node pNode = pListHead;
        while(pNode->next != pToBeDeleted)
        {
            pNode = pNode->next;            
        }

        pNode->next = NULL;
        delete pToBeDeleted;
        pToBeDeleted = NULL;
    }
}

我们分析一下这个思路的时间复杂度。对于n-1个非尾结点而言，我们可以在O(1)时把下一个结点的内存复制覆盖要删除的结点，并删除下一个结点；对于尾结点而言，由于仍需要顺序查找，时间复杂度为O(n).因此总的时间复杂度为[(n-1)*O(1)+O(n)]/n,结果仍然是O(1),符合要求。

题目：输入一个整数，求该整数的二进制表达中有多少个1。例如输入10，由于其二进制表示为1010，有两个1，因此输出2。

##可能引起死循环的解法
一个很基本的想法是，我们先判断整数的最右边一位是不是1。接着把整数右移一位，原来处于右边第二位的数字现在被移到第一位了，再判断是不是1。这样每次 移动一位，直到这个整数变成0为止。现在的问题变成怎样判断一个整数的最右边一位是不是1了。很简单，如果它和整数1作与运算。由于1除了最右边一位以 外，其他所有位都为0。因此如果与运算的结果为1，表示整数的最右边一位是1，否则是0。

代码如下：

///////////////////////////////////////////////////////////////////////
// Get how many 1s in an integer's binary expression
///////////////////////////////////////////////////////////////////////
int NumberOf1_Solution1(int i)
{
      int count = 0;
      while(i)
      {
            if(i & 1)
                  count ++;
            i = i >> 1;
      }
      return count;
}

面试官会问，整数右移一位在数学上是和除以2是等价的。那可不可以把上面的代码中的右移运算符换成除以2呢？答案是否定的。因为除法的效率比移位运算要低的多，在实际编程中如果可以，应尽可能地用移位运算符代替乘除法。

这个思路当输入i是正数时没有问题，但当输入的i是一个负数时，不但不能得到正确的1的个数，还将导致死循环。以负数0x80000000为例，右移一位 的时候，并不是简单地把最高位的1移到第二位变成0x40000000，而是0xC0000000。这是因为移位前是个负数，仍然要保证移位后是个负数， 因此移位后的最高位会设为1。如果一直做右移运算，最终这个数字就会变成0xFFFFFFFF而陷入死循环。

##改进算法避免死循环
为了避免死循环，我们可以不右移输入的数字i。首先i和1做与运算，判断i的最低位是不是为1。接着把1左移一位得到2，再和i做与运算，就能判断i的次高位是不是1……这样反复左移，每次都能判断i的其中一位是不是1。基于此，我们得到如下代码：

///////////////////////////////////////////////////////////////////////
// Get how many 1s in an integer's binary expression
///////////////////////////////////////////////////////////////////////
int NumberOf1_Solution2(int i)
{
      int count = 0;
      unsigned int flag = 1;
      while(flag)
      {
            if(i & flag)
                  count ++;
            flag = flag << 1;
      }
      return count;
}

##给面试官带来惊喜的解法
另外一种思路是如果一个整数不为0，那么这个整数至少有一位是1。如果我们把这个整数减去1，那么原来处在整数最右边的1就会变成0，原来在1后面的所有 的0都会变成1。其余的所有位将不受到影响。举个例子：一个二进制数1100，从右边数起的第三位是处于最右边的一个1。减去1后，第三位变成0，它后面 的两位0变成1，而前面的1保持不变，因此得到结果是1011。

我们发现减1的结果是把从最右边一个1开始的所有位都取反了。这个时候如果我们再把原来的整数和减去1之后的结果做与运算，从原来整数最右边一个1那一位 开始所有位都会变成0。如1100&1011=1000。也就是说，把一个整数减去1，再和原整数做与运算，会把该整数最右边一个1变成0。那么 一个整数的二进制有多少个1，就可以进行多少次这样的操作。

这种思路对应的代码如下：

///////////////////////////////////////////////////////////////////////
// Get how many 1s in an integer's binary expression
///////////////////////////////////////////////////////////////////////
int NumberOf1_Solution3(int i)
{
      int count = 0;
      while (i)
      {
            ++ count;
            i = (i - 1) & i;
      }
      return count;
}

##扩展
扩展1：如何用一个语句判断一个整数是不是二的整数次幂？

思路：一个整数如果是2的整数次方，那么它的二进制表示中有且只有一位是1，而其他所有位都是0.根据前面的分析，把这个整数减去1之后再和它自己做与运算，这个整数中唯一的1就会变成0.

n&(n-1)==0;//二进制数只有一位位1，则该数是2的整数次幂.

扩展2：输入两个整数m和n，计算需要改变m的二进制表示中的多少位才能得到n。比如10的二进制表示为1010,13的二进制表示为1101，需要改变1010中的3位才能得到1101.

思路：我们可以分两步解决这个问题：第一步求这两个数的异或，第二步统计异或结果中1的位数。

##总结
把一个整数减去1之后再和原来的整数做位与运算，得到的结果相当于是把整数的二进制表示中的最后一个1变成0.很多二进制的问题都可以用这个思路解决

##递归解法
教课书上一般都是用斐波拉切数列来说明递归，但是用递归的方法来求解斐波拉切数列并不是一个好的方法，这主要是效率的问题。

long fibonacci(unsigned int n)
{
    if(n <= 0)
        return 0;

    if(n == 1)
        return 1;

    return fibonacci(n - 1) + fibonacci(n - 2);
}

这个方法的低效体现在哪里呢？我们不妨来分析一下fibnacci(8)的求解过程：

我们不难发现在这棵树中很多结点是重复的，而且重复的结点数会随着n的增大而急剧增加，这意味着计算量会随着n的睁大而急剧增大。事实上，用递归计算的时间复杂度是以n的指数的方式递增的。

##循环解法
在这里，递归的缺陷在于重复计算了很多项，为了避免重复计算，我们可以使用循环：

long fibonacci_iterator(unsigned int n)
{
    int result[2] = {0, 1};
    if(n < 2)
        return result[n];

    long fib_one = 0;
    long fib_two = 1;

    long fib_num = 0;
    int i;
    for(i = 2; i <= n; i++) {
        fib_num = fib_one + fib_two;
        fib_one = fib_two;
        fib_two = fib_num;
    }

    return fib_num;
}

##测试程序

#define n 50
int main(int argc, char **argv)
{
    clock_t start, end;
    double times = 0;

    start = clock();
    printf("fibonacci(%d) = %d\n", n, fibonacci(n));
    end = clock();
    times = (double)(end - start) / CLOCKS_PER_SEC;
    printf("The fibonacci took %fs\n", times);
    start = clock();
    printf("fibonacci(%d) = %d\n", n, fibonacci_iterator(n));
    end = clock();
    times = (double)(end - start) / CLOCKS_PER_SEC;
    printf("The fibonacci_iterator took %fs\n", times);
}

输出为:

fibonacci(50) = 12586269025

The fibonacci took 203.040000s

fibonacci(50) = 12586269025

The fibonacci_iterator took 0.000000s

所以说，在这里用递归的话真是脑子被门夹了

##题目

输入某二叉树的前序遍历和中序遍历的结果，请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字，例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}，应该重构出如下二叉树：

##答案

• 前序遍历的第一个节点是树的根结点，所以1是树的根结点
• 中序遍历的规则是：1.遍历左子树；2.根结点；3.遍历右子树。既然1是根结点，那么从中序遍历的输出可知：4,7,2在左子树中，5,3,8,6在右子树中
• 前序遍历输出的第二个值是根结点的左子树的根结点，即2是左子树序列4,7,2的根结点，而在2左侧的4,7就是根结点2的左子树中的值了。同理3是根结点的右子树的根结点，5是以3为根结点的树的左子树中的值，8,6是右子树中的值
• 下面只需要判断左子树中4,7和右子树中8,6的位置就可以了，易知，4是2的左儿子，7是4的右儿子。6是3的右儿子，8是6的左儿子。
• 这是一个递归的过程，没分析一段，就将这一段当做一个完整的树来分析就很容易了

实现的代码在这里Construct

sizeof

问：C++里定义一个空的类型，里面没有任何成员变量和成员函数。对该类型求sizeof，得到的结果是多少？

答：1

问：为什么不是0？

答：空类型的实例中不包含任何信息，本来求sizeof应该是0，但是当我们声明该类型的实例的时候，它必须在内存中占有一定的空间，否则无法使用这些实例。至于占用多少内存，由编译器决定。Visual Studio中每个空类型的实例占用1字节的空间。

问：如果在该类型中添加一个构造函数和析构函数，再对该类型求sizeof，得到的结果又是多少？

答：和前面一样，还是1。调用构造函数和析构函数只需要知道函数的地址即可，而这些函数的地址只与类型相关，而与类型的实例无关，编译器也不会因为这两个函数而在实例内添加任何额外的信息。

问：那如果把析构函数标记为虚函数呢？

答：C++编译器一旦发现一个类型中有虚函数，就会为该类型生成虚函数表，并在该类型的每一个实例中添加一个虚函数表的指针。在32位的机器上，一个指针占4字节的空间，因此求sizeof得到4；如果是64位的机器，一个指针占8字节的空间，因此求sizeof则得到8。

数组与指针

运行下面的代码，结果是什么？

int _tmain(int argc, _TCHAR* argv[])
{
    char str1[] = "hello world";
    char str2[] = "hello world";

    char* str3 = "hello world";
    char* str4 = "hello world";

    if(str1 == str2)
        printf("str1 and str2 are same.\n");
    else
        printf("str1 and str2 are not same.\n");

    if(str3 == str4)
        printf("str3 and str4 are same.\n");
    else
        printf("str3 and str4 are not same.\n");

    return 0;
}

str1和str2是两个字符串数组，我们会为它们分配两个长度为12个字节的空间，并把”hello world”的内容分别复制到数组中去。这是两个初始地址不同的数组，因此str1和str2的值也不相同，所以输出的第一行是”str1 and str2 are not same”。

str3和str4是两个指针，我们无须为它们分配内存以存储字符串的内容，而只需要把它们指向”hello world”在内存中的地址就可以了。由于“hello world”是常量字符串，它在内存中只有一个拷贝，因此str3和str4指向的是同一个地址。所以比较str3和str4的值得到的结果是相同的，输出的第二行是”str3 and str4 are same”。

关于(&a + 1)和*(a + 1)

main()
{
int a[5]={1,2,3,4,5};
int *ptr=(int *)(&a+1);
printf("%d,%d",*(a+1),*(ptr-1));
}

程序输出为：2,5

解释：

*(a+1)其实很简单就是指a[1],输出为2.

问题关键就在于第二个点，*(ptr-1)输出为多少？

解释如下，&a+1不是首地址+1，系统会认为加了一个整个a数组，偏移了整个数组a的大小（也就是5个int的大小）。所以int *ptr=(int *)(&a+1);其实ptr实际是&(a[5]),也就是a+5.

原因为何呢？

&a是数组指针，其类型为int(*)[5];
而指针加1要根据指针类型加上一定的值，不同类型的指针+1之后增加的大小不同，a是长度为5的int数组指针，所以要加5*sizeof(int)，所以ptr实际是a[5],但是ptr与（&a+1）类型是不一样的，这点非常重要，所以ptr-1只会减去sizeof(int*),a，&a的地址是一样的，但意思就不一样了，a是数组首地址，也就是a[0]的地址，&a是对象（数组）首地址，a+1是数组下一元素的地址，即a[1],&a+1是下一个对象的地址，即a[5]。

##概念
c语言中存在两类整数算术运算，有符号运算和无符号运算。在无符号运算里，没有了符号位，所以是没有溢出的概念的。

所有的无符号运算都是以2的n次方为模。如果算术运算符的一个操作数是有符号数，另一个是无符号数，那么有符号数会被转换为无符号数(表示范围小的总是被转换为表示范围大的)，那么溢出也不会发生。但是，当两个操作数都是有符号数时，溢出就有可能发生。而且溢出的结果是未定义的。当一个运算的结果发生溢出时，任何假设都是不安全的。

##如何检测溢出
例如，假定a和b是两个非负的整型变量(有符号)，我们需要检查a+b是否溢出，一种想当然的方式是:

if (a + b < 0)
溢出

实际上，在现实世界里，这并不能正常运行。当a+b确实发生溢出时，所有关于结果如何的假设均不可靠。比如，在某些机器的cpu，加法运算将设置一个内部寄存器为四种状态:正，负，零和溢出。在这种机器上，c编译器完全有理由实现以上的例子，使得a+b返回的不是负，而是这个内存寄存器的溢出状态。显然，if的判断会失败。

一种正确的方式是将a和b都强制转换为无符号整数：

if ( (unsigned)a + (unsigned)b  > INT_MAX)
溢出

这里的INT_MAX值为有符号整型的最大值。在一般的编译器里是一个预定义的常量。ANSI C在limits里定义了INT_MAX，值为

2的31次方 - 1.

不需要用到无符号算数运算的另一种可行方法是：

if (a > INT_MAX - b)
溢出

PS : 有符号数的最高位(31位)为符号位，最高位为0的时候，表示正，为1的时候表示负。运算时，符号位不参加运算，但是如果两个数相加，30位需要进1时，那么即表示溢出。

##代码

#include<stdio.h>
#include<stdlib.h>
#include<string.h>
void GetMemory(char **p,int num)
{
    *p = malloc(num);
}
int main()
{
    char *str = NULL;   
    GetMemory(&str, 100);   

    strcpy(str, "hello");   
    free(str);

    if (str != NULL)
    {
        strcpy(str, "world");
    }   
    printf("\n str is %s", str);
    getchar();
}

打印出来的结果是：str is world

##解释
本题主要考察了对free的理解，总结一下就是3点

• free只是释放了malloc所申请的内存，并不改变指针的值
• 由于指针所指向的内存已经被释放，所以其它代码有机会改写其中的内容，相当于该指针从此指向了自己无法控制的地方，也称为野指针
• 为了避免失误，最好在free之后，将指针指向NULL

1. 目录在linux文件系统中是以怎样的形式存在的：文件
2. 通过文件名存取文件时，文件系统内部的操作过程是通过:文件名在目录中查找对应的i节点，通过i节点存取文件数据。
3. 关于文件block，以下说法是正确的：
   • 文件系统中存储的最小单位是块（Block）
   • block越大，inode越少，适合存储文件大而少的文件系统
   • block块可以用mkfs.ext3 -b来制定块的大小
   • 每个block最多存放一个文件，而当一个block存放不下的情况下，会占用下一个block
4. 同一进程下的线程可以共享：data section，file fd，不可以共享：stack，register set
5. 线程，进程，多任务：
   • 线程是指进程内的一条执行线路，或者说是进程中可执行代码的单独单元，它是操作系统的基本调度单元。
   • 一个进程至少有一个线程，即主线程，也可以有多个线程协同工作。
   • 进程从主线程开始执行，进而可以创建一个或多个附加线程来执行该进程内的并发任务，这就是基于线程的多任务。
   • 线程和进程都可并发执行
   • 在linux系统中，线程是处理器调度的基本单位
   • 线程的粒度小于进程，通常多线程比多进程并发性更高

##概念分析
LRU(Least Recent Used):最近最少使用，就是将最近最少使用的页淘汰掉，替换为新的页。核心思想是：如果一个页最近被访问了，那他之后被访问的概率也高；如果一个页最近没有被访问，那他之后也不会被访问。这道理其实说不通哈，但是LRU算法确实解决页访问的效率问题。

##原理
下面是一个应用LRU算法的例子的流程图

下面简单讲解一下(需要在这里说明一下,LRU一般采用链表方式实现,便于快速移动数据位置,虽然图中使用似乎是数组方式):

• 一开始,缓存池是空的,缓存池中插入数据时不用担心容量不足的事情.因此这个过程就是类似队列的FIFO(但不止这些);
• 在第5步将E插入到缓存池中后,缓存池已经满了(当然实际应用中不会让到达缓存池的尺寸,一般到70%左右就要考虑淘汰机制了);
• 当第6步将E插入缓存池的时候,发现缓存池已经满了,LRU会将最早加入到缓存池的数据淘汰掉(A,实在不要意思啊);
• 第7步,从缓存池中访问C,C被访问,从时间点上是最近最近访问的,将C移动到链表的头部(C侥幸暂时远离被淘汰的边缘);
• 第8步,将G插入缓存池中,G处于链表头部,B不幸被淘汰.

大致的过程就是这样,关于淘汰机制只是后面的三步中会用到,画出前面六步的过程只是说明LRU插入元素的方式.在这个图中,我想大家应该可以明白为什么使用链表,而不使用数组(链表的插入和删除的时间复杂度都是O(1)).

##优劣分析

###命中率
命中率较高,不过偶发性的情况对LRU的命中影响很大,同时也会引入很多数据污染

###复杂度
实现起来较为简单.

###存储成本
几乎没有空间上浪费.

###缺陷
仅仅从最近使用时间上考虑淘汰算法,没有考虑缓存单元的使用频率,可能会淘汰一些仍有价值的单元.