为什么求斐波拉切数列用递归不是一个好方法

##递归解法
教课书上一般都是用斐波拉切数列来说明递归，但是用递归的方法来求解斐波拉切数列并不是一个好的方法，这主要是效率的问题。

long fibonacci(unsigned int n)
{
    if(n <= 0)
        return 0;

    if(n == 1)
        return 1;

    return fibonacci(n - 1) + fibonacci(n - 2);
}

这个方法的低效体现在哪里呢？我们不妨来分析一下fibnacci(8)的求解过程：

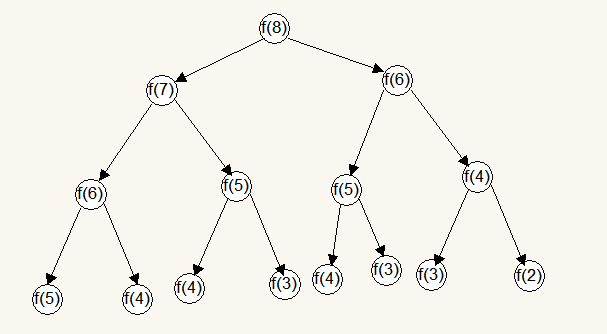
我们不难发现在这棵树中很多结点是重复的，而且重复的结点数会随着n的增大而急剧增加，这意味着计算量会随着n的睁大而急剧增大。事实上，用递归计算的时间复杂度是以n的指数的方式递增的。

##循环解法
在这里，递归的缺陷在于重复计算了很多项，为了避免重复计算，我们可以使用循环：

long fibonacci_iterator(unsigned int n)
{
    int result[2] = {0, 1};
    if(n < 2)
        return result[n];

    long fib_one = 0;
    long fib_two = 1;

    long fib_num = 0;
    int i;
    for(i = 2; i <= n; i++) {
        fib_num = fib_one + fib_two;
        fib_one = fib_two;
        fib_two = fib_num;
    }

    return fib_num;
}

##测试程序

#define n 50
int main(int argc, char **argv)
{
    clock_t start, end;
    double times = 0;

    start = clock();
    printf("fibonacci(%d) = %d\n", n, fibonacci(n));
    end = clock();
    times = (double)(end - start) / CLOCKS_PER_SEC;
    printf("The fibonacci took %fs\n", times);
    start = clock();
    printf("fibonacci(%d) = %d\n", n, fibonacci_iterator(n));
    end = clock();
    times = (double)(end - start) / CLOCKS_PER_SEC;
    printf("The fibonacci_iterator took %fs\n", times);
}

输出为:

fibonacci(50) = 12586269025

The fibonacci took 203.040000s

fibonacci(50) = 12586269025

The fibonacci_iterator took 0.000000s

所以说，在这里用递归的话真是脑子被门夹了