##题目
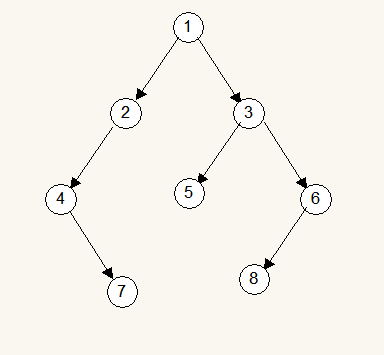
输入某二叉树的前序遍历和中序遍历的结果,请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字,例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6},应该重构出如下二叉树:
##答案
- 前序遍历的第一个节点是树的根结点,所以
1是树的根结点 - 中序遍历的规则是:1.遍历左子树;2.根结点;3.遍历右子树。既然1是根结点,那么从中序遍历的输出可知:
4,7,2在左子树中,5,3,8,6在右子树中 - 前序遍历输出的第二个值是根结点的左子树的根结点,即
2是左子树序列4,7,2的根结点,而在2左侧的4,7就是根结点2的左子树中的值了。同理3是根结点的右子树的根结点,5是以3为根结点的树的左子树中的值,8,6是右子树中的值 - 下面只需要判断左子树中
4,7和右子树中8,6的位置就可以了,易知,4是2的左儿子,7是4的右儿子。6是3的右儿子,8是6的左儿子。 - 这是一个递归的过程,没分析一段,就将这一段当做一个完整的树来分析就很容易了
实现的代码在这里Construct